Knot Groups

This page is mostly an excuse to show off something cool I made during my summer working with Ben Williams that wouldn’t show up in the paper. At one point during the summer, I was studying how the symmetries of knot 9-48 act on its corresponding fundamental group. Generally the way you do this is quite geometric, just draw out the generating loops of the fundamental group and see where they end up under the symmetric transformation. The issue is that this doesn’t work with knot 9-48, as there are no symmetries of the knot that can be seen in R^3 alone. We instead need to work with R^3 with an added point at infinity, and symmetries that look like this.

My solution to this was simple, but very time-consuming: Create a 3d graphing program which plotted surfaces and curves projected into R^3 from S^3, using coordinates for S^3, and use these coordinates to more easily apply the required transformations. The early tests of this were with a much simpler (5,2)-torus knot.

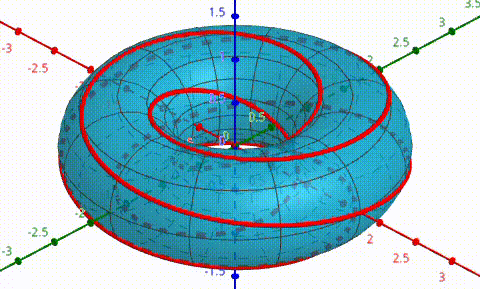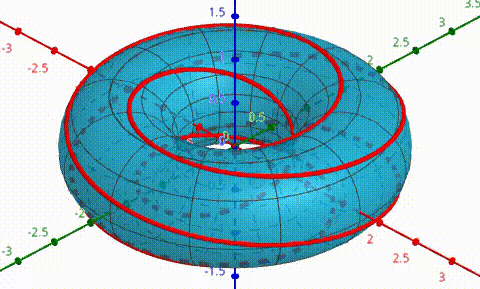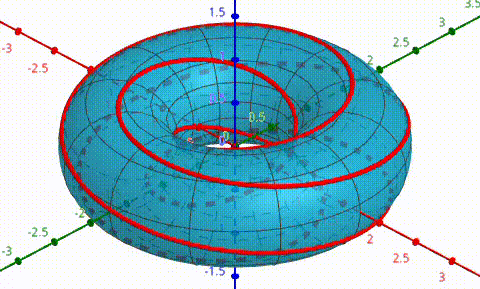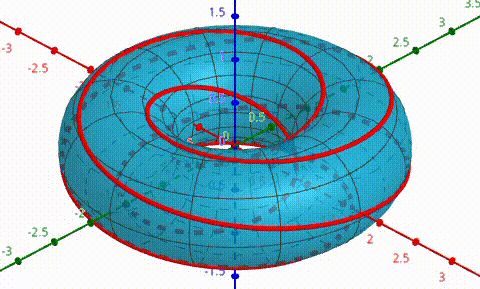
After this, I applied the program to knot 9-48 with an extra rotation about the z-axis.

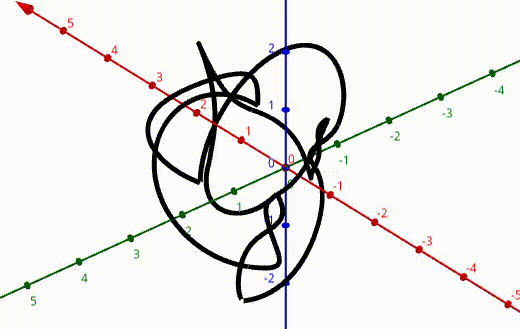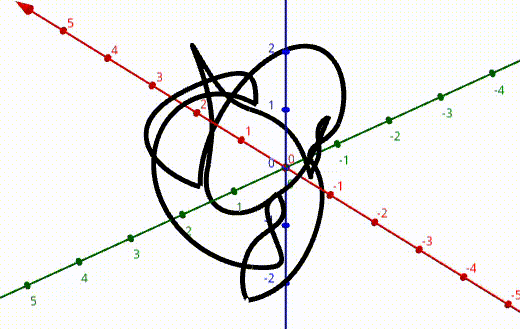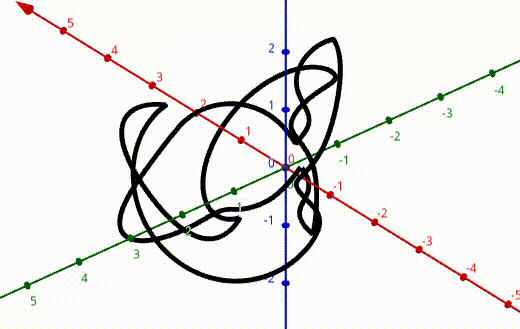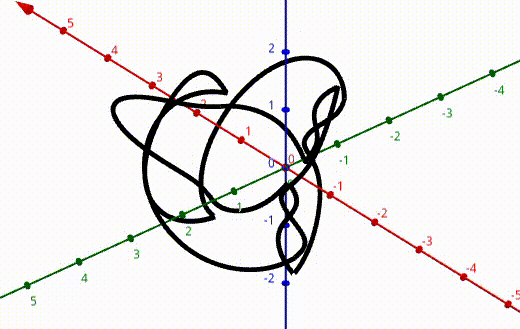
Using this, I was able to determine the action of this transformation on the corresponding knot group for knot 9-48. If you’re interested in the gritty details (along with all the rest of the calculations I did that summer) see the pdf at the top of the page.

I’ll end this off with a couple of links. The finished product for knot 9-48, and a template for those of you crazy enough to try and do something like this yourself. The plan that summer was actually to apply this again to ten crossing knots, but there didn’t end up being enough time for it.